Для того, чтобы мне опровергнуть ваше решение или наоборот согласиться с ним, достаточно всего лишь разобраться в одном вопросе:
PSP, вы согласны, что что для того, чтобы разнос Шуршавчика был максимальным, нужно, чтобы он обязательно "посетил" координату -77?
Если да, то координату -77 можно достичь одним способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой которой разнос Шуршавчика максимальный.
Если нет, то жду примера, в котором разнос равен 123 и Шуршавчик не посетил координату -77.
Комбинаторика и вероятность...
Модератор: модераторы
Re: Комбинаторика и вероятность...
Последний раз редактировалось LNV Пн, 22 янв 2018, 22:29, всего редактировалось 2 раза.
Re: Комбинаторика и вероятность...
PSP писал(а):LNV писал(а):Наибольший разнос получается, если все шаги вправо Шуршавчик делает подряд
Замечу, что эта фраза эквивалента фразе из моего решения: "Очевидно, что разнос будет максимальным только в том случае, если каждую точку в разносе (отрезке) Шуршавчик пройдёт не более 2-х раз" (то есть он не делает петель) - которую PSP подчеркнул, и написал, что это не очевидно, хотя сейчас пишет тоже самое.
"Эквивалентность" и "то же самое" - это не одно и то же. И , тем более, далеко не всегда эквивалентность очевидна.
Правильно ли я понимаю, что Вы согласились с тем, что моя фраза из моего решения, эта та же фраза, что и их вашего?
Если правильно, то тогда баллов, как минимум за это, прибавить-то надо.
-
PSP
- Администратор сайта
- Сообщения: 7201
- Зарегистрирован: Вс, 28 дек 2003, 11:47
- Откуда: Луга
- Контактная информация:
Re: Комбинаторика и вероятность...
LNV писал(а):Для того, чтобы мне опровергнуть ваше решение или наоборот согласиться с ним, достаточно всего лишь разобраться в одном вопросе:
PSP, вы согласны, что что для того, чтобы разнос Шуршавчика был максимальным, нужно, чтобы он обязательно "посетил" координату -77?
Если да, то координату -77 можно достичь одним способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой которой разнос Шуршавчика максимальный.
Если нет, то жду примера, в котором разнос равен 123 и Шуршавчик не посетил координату -77.
Неправильная логика.
Для того чтобы согласиться или опровергнуть выложенное решение, безусловно, необходимо, его понять.
А затем можно
- задать вопрос по решению (а не какой-либо вообще);
- опровергнуть ту или иную часть решения.
-
PSP
- Администратор сайта
- Сообщения: 7201
- Зарегистрирован: Вс, 28 дек 2003, 11:47
- Откуда: Луга
- Контактная информация:
Re: Комбинаторика и вероятность...
LNV писал(а):Правильно ли я понимаю, что Вы согласились с тем, что моя фраза из моего решения, эта та же фраза, что и их вашего?
Нет. Если утверждается, что одно утверждение равносильно (эквивалентно) другому, это следует доказать.
Мне эквивалентность не очевидна.
Re: Комбинаторика и вероятность...
Я повторю вопрос:
PSP, вы согласны, что что для того, чтобы разнос Шуршавчика был максимальным, нужно, чтобы он обязательно "посетил" координату -77?
Если да, то координату -77 можно достичь одним способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой которой разнос Шуршавчика максимальный.
Если нет, то жду примера, в котором разнос равен 123 и Шуршавчик не посетил координату -77.
PSP, вы согласны, что что для того, чтобы разнос Шуршавчика был максимальным, нужно, чтобы он обязательно "посетил" координату -77?
Если да, то координату -77 можно достичь одним способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой которой разнос Шуршавчика максимальный.
Если нет, то жду примера, в котором разнос равен 123 и Шуршавчик не посетил координату -77.
-
PSP
- Администратор сайта
- Сообщения: 7201
- Зарегистрирован: Вс, 28 дек 2003, 11:47
- Откуда: Луга
- Контактная информация:
Re: Комбинаторика и вероятность...
LNV писал(а):Я повторю вопрос:
PSP, вы согласны, что что для того, чтобы разнос Шуршавчика был максимальным, нужно, чтобы он обязательно "посетил" координату -77?
Нет необходимости повторять один и тот же вопрос.
А мне приходится повторить: утверждения в математике должны доказываться. Чьё-то согласие или несогласие не имеет никакого значения.
Где док-во сформулированного утверждения?
Возражать можно доказательству. А его просто нет. Процитированное выше утверждения для меня НЕ ОЧЕВИДНО.
САМОЕ ГЛАВНОЕ
Есть возражения против выложенного решения или нет?
Если LNV знает иное решение, дающее отличный от моего ответ, то это уже другая тема (другая задача).
-
PSP
- Администратор сайта
- Сообщения: 7201
- Зарегистрирован: Вс, 28 дек 2003, 11:47
- Откуда: Луга
- Контактная информация:
Re: Комбинаторика и вероятность...
Давайте обсудим ДОПОЛНИТЕЛЬНУЮ ЗАДАЧУ, судя по всему, понравившуюся LNV.
ДОПОЛНИТЕЛЬНАЯ ЗАДАЧА
Давайте предположим, что следующее утверждение истинное:
для того чтобы разнос Шуршавчика был максимальным, необходимо, чтобы он обязательно побывал в точке с координатой -77
(это несколько отредактированное утверждение LNV).
Истинно ли тогда рассуждение LNV:
точку с координатой -77 можно достичь единственным способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой разнос Шуршавчика максимальный
(это немного откорректированное утверждение LNV)?
Правда, тому, кто будет думать над дополнительной задачей, придётся догадаться, что означает выражение LNV
"чередуя вначале все шаги влево".
Возможно, сам LNV заменит это выражение на нечто русское понятное (ведь чередовать можно только что-то с чем-то).
LNV писал(а):PSP, вы согласны, что что для того, чтобы разнос Шуршавчика был максимальным, нужно, чтобы он обязательно "посетил" координату -77?
Если да, то координату -77 можно достичь одним способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой которой разнос Шуршавчика максимальный.
ДОПОЛНИТЕЛЬНАЯ ЗАДАЧА
Давайте предположим, что следующее утверждение истинное:
для того чтобы разнос Шуршавчика был максимальным, необходимо, чтобы он обязательно побывал в точке с координатой -77
(это несколько отредактированное утверждение LNV).
Истинно ли тогда рассуждение LNV:
точку с координатой -77 можно достичь единственным способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой разнос Шуршавчика максимальный
(это немного откорректированное утверждение LNV)?
Правда, тому, кто будет думать над дополнительной задачей, придётся догадаться, что означает выражение LNV
"чередуя вначале все шаги влево".
Возможно, сам LNV заменит это выражение на нечто русское понятное (ведь чередовать можно только что-то с чем-то).
Re: Комбинаторика и вероятность...
PSP писал(а):LNV писал(а):Я повторю вопрос:
PSP, вы согласны, что что для того, чтобы разнос Шуршавчика был максимальным, нужно, чтобы он обязательно "посетил" координату -77?
Нет необходимости повторять один и тот же вопрос.
А мне приходится повторить: утверждения в математике должны доказываться. Чьё-то согласие или несогласие не имеет никакого значения.
Где док-во сформулированного утверждения?
Возражать можно доказательству. А его просто нет. Процитированное выше утверждения для меня НЕ ОЧЕВИДНО.
Я даже больше скажу, оно НЕВЕРНО!
Контрпример: Шуршавчик сделал все ходы вправо, а затем все ходы влево, при этом его разнос - 123.
PSP писал(а):САМОЕ ГЛАВНОЕ
Есть возражения против выложенного решения или нет?
Если LNV знает иное решение, дающее отличный от моего ответ, то это уже другая тема (другая задача).
Я, наконец, понял его (решение)! Возражений больше нет.
Замечу, что если PSP написал бы хотя бы тот контрпример, который привёл я, то дело пошло куда быстрее.
Re: Комбинаторика и вероятность...
PSP писал(а):Давайте обсудим ДОПОЛНИТЕЛЬНУЮ ЗАДАЧУ, судя по всему, понравившуюся LNV.
ДОПОЛНИТЕЛЬНАЯ ЗАДАЧА
Давайте предположим, что следующее утверждение истинное:
для того чтобы разнос Шуршавчика был максимальным, необходимо, чтобы он обязательно побывал в точке с координатой -77
(это несколько отредактированное утверждение LNV).
Истинно ли тогда рассуждение LNV:
точку с координатой -77 можно достичь единственным способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой разнос Шуршавчика максимальный
(это немного откорректированное утверждение LNV)?
Правда, тому, кто будет думать над дополнительной задачей, придётся догадаться, что означает выражение LNV
"чередуя вначале все шаги влево".
Возможно, сам LNV заменит это выражение на нечто русское понятное (ведь чередовать можно только что-то с чем-то).
Безусловно, я имел в виду, что Шуршавчик делает первые 77 ходов влево.
Я считаю, что моё утверждение истинно.
-
PSP
- Администратор сайта
- Сообщения: 7201
- Зарегистрирован: Вс, 28 дек 2003, 11:47
- Откуда: Луга
- Контактная информация:
Re: Комбинаторика и вероятность...
Быстрее - не значит полезнее.LNV писал(а):Замечу, что если PSP написал бы хотя бы тот контрпример, который привёл я, то дело пошло куда быстрее.
Излагать на математическом форуме нечто с той же степенью "разжёванности", что в обычных школьных учебниках? От этого пользы будет очень мало. А так - куда полезнее. Например, для LNV уж точно полезнее.
Re: Комбинаторика и вероятность...
[Дубль сообщения]
Последний раз редактировалось BIA Сб, 10 авг 2019, 12:25, всего редактировалось 1 раз.
Re: Комбинаторика и вероятность...
Пользуясь великим экстрасенсорным даром "Ответчика за 5 первых секунд от объявления условия" я всё же полагаю, что LNV, говоря "чередуя вначале все шаги влево" имел ввиду, что любая полная последовательность шагов, совершённых шуршавчиком, может быть преобразована таким образом, что сначала записаны все шаги влево, а затем все шаги вправо. Но это не относится к решению задачи.
Это неверное утверждение, т.к. последовательность [Все влево | Затем все вправо], даёт разницу в координатах 123 (-77 .. 46), ровно как и [Все вправо | Затем все влево] - тоже разница 123 (0 .. 123).
Говорить об истинности этого утверждения некорректно, имея неверный посыл. Но погрузимся в него, так как предыдущее предложение чистая демагогия. Наше выражение (A => B) состоит из трёх частей:
1. A : "Точку с координатой -77 можно достичь единственным способом" - Истина (все шаги влево, никак иначе)
2. B : "Существует всего одна последовательность шагов, при которой разнос Шуршавчика максимальный" - Ложь (выше контр-пример, предоставленный и до меня)
3. A implies B, A => B : " *A* , следовательно, *B*" - Ложь
Обратимся к авторитетному источнику, ну, например, интернету
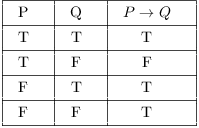
Нетрудно заметить, что в таблице истинности единственное значение Ложь в операции A implies B ( A => B ) достигается в случае, когда A - истинно, а B - ложно, как раз наш случай.
Но имеется нюанс в виде "предположительной" истинности утверждения C : "для того чтобы разнос Шуршавчика был максимальным, необходимо, чтобы он обязательно побывал в точке с координатой -77"
Безотносительно истинности C, рассмотрим два случая, когда C истинно и когда C ложно. Обновим наше выражение, теперь оно выглядит так:
* : (A and C) => B
Не поленимся и напишем таблицу истинности для A and C
A | C | A and C
T | T | T
T | F | F
F | T | F
F | F | F
Из неё нас интересуют только первые 2 строчки, поскольку выше мы заметили, что А - истинно.
Итого у нас две ситуации:
1. Истина => Ложь (Ложь)
2. Ложь => Ложь (Истина)
Суть™ показанного мною заключается в том, что оператор => не подразумевает какой-либо связи между левой и правой частями выражения. В доказательствах очень опасно использовать следствие и не так много случаев, где оно действительно помогает, в отличии от равносильности. Но если отбросить эмоционально-предупредительную сторону и посмотреть на более расширенное выражение:
( ( A and C ) => B ) <=> B, то можно заметить, что это выражение не всегда истинно, что и делает его опасным для использования в доказательствах. Совсем другое дело (A and C) <=> B, в таком виде гораздо заметнее логическая ошибка.
Я бы предложил прочитавшим сей пост самостоятельно переформулировать сюжет №2 для тренировки понятия "равносильно" =)
Простите за внимание ^^
"для того чтобы разнос Шуршавчика был максимальным, необходимо, чтобы он обязательно побывал в точке с координатой -77"
Это неверное утверждение, т.к. последовательность [Все влево | Затем все вправо], даёт разницу в координатах 123 (-77 .. 46), ровно как и [Все вправо | Затем все влево] - тоже разница 123 (0 .. 123).
"точку с координатой -77 можно достичь единственным способом (чередуя вначале все шаги влево), следовательно, существует всего одна последовательность шагов, при которой разнос Шуршавчика максимальный"
Говорить об истинности этого утверждения некорректно, имея неверный посыл. Но погрузимся в него, так как предыдущее предложение чистая демагогия. Наше выражение (A => B) состоит из трёх частей:
1. A : "Точку с координатой -77 можно достичь единственным способом" - Истина (все шаги влево, никак иначе)
2. B : "Существует всего одна последовательность шагов, при которой разнос Шуршавчика максимальный" - Ложь (выше контр-пример, предоставленный и до меня)
3. A implies B, A => B : " *A* , следовательно, *B*" - Ложь
Обратимся к авторитетному источнику, ну, например, интернету

Нетрудно заметить, что в таблице истинности единственное значение Ложь в операции A implies B ( A => B ) достигается в случае, когда A - истинно, а B - ложно, как раз наш случай.
Но имеется нюанс в виде "предположительной" истинности утверждения C : "для того чтобы разнос Шуршавчика был максимальным, необходимо, чтобы он обязательно побывал в точке с координатой -77"
Безотносительно истинности C, рассмотрим два случая, когда C истинно и когда C ложно. Обновим наше выражение, теперь оно выглядит так:
* : (A and C) => B
Не поленимся и напишем таблицу истинности для A and C
A | C | A and C
T | T | T
T | F | F
F | T | F
F | F | F
Из неё нас интересуют только первые 2 строчки, поскольку выше мы заметили, что А - истинно.
Итого у нас две ситуации:
1. Истина => Ложь (Ложь)
2. Ложь => Ложь (Истина)
Суть™ показанного мною заключается в том, что оператор => не подразумевает какой-либо связи между левой и правой частями выражения. В доказательствах очень опасно использовать следствие и не так много случаев, где оно действительно помогает, в отличии от равносильности. Но если отбросить эмоционально-предупредительную сторону и посмотреть на более расширенное выражение:
( ( A and C ) => B ) <=> B, то можно заметить, что это выражение не всегда истинно, что и делает его опасным для использования в доказательствах. Совсем другое дело (A and C) <=> B, в таком виде гораздо заметнее логическая ошибка.
Я бы предложил прочитавшим сей пост самостоятельно переформулировать сюжет №2 для тренировки понятия "равносильно" =)
Простите за внимание ^^
-
PSP
- Администратор сайта
- Сообщения: 7201
- Зарегистрирован: Вс, 28 дек 2003, 11:47
- Откуда: Луга
- Контактная информация:
Re: Комбинаторика и вероятность...
BIA писал(а):Простите за внимание ^^
В прощении необходимости нет по причине отсутствия события для прощения.
Спасибо, BIA, за внимание!
Полагаю, LNV есть что сказать...
Думаю, имею право сообщить "городу и миру", что BIA и LNV - мои бывшие ученики.
Впрочем, покойный академик С. С. Лавров как-то сказал, помогая мне на устной олимпиаде Ленинградской ЮМШ: "Бывших учеников не бывает, Серёжа".
Продолжаю считать себя учеником Святослава Сергеевича.
Re: Комбинаторика и вероятность...
На самом деле, LNV сказать нечего. Прошло уже больше года...
Всё, что припоминаю про эту задачу: я тогда разобрался со всеми своими косяками и признал решение PSP (и даже ему об этом сообщим при личной встрече). Просто публично на сайте не признался
Глюки бывают у всех...
Безусловно, большое спасибо BIA за такую хорошую рецензию!
Всё, что припоминаю про эту задачу: я тогда разобрался со всеми своими косяками и признал решение PSP (и даже ему об этом сообщим при личной встрече). Просто публично на сайте не признался
Глюки бывают у всех...
Безусловно, большое спасибо BIA за такую хорошую рецензию!
-
PSP
- Администратор сайта
- Сообщения: 7201
- Зарегистрирован: Вс, 28 дек 2003, 11:47
- Откуда: Луга
- Контактная информация:
Re: Комбинаторика и вероятность...
LNV писал(а):На самом деле, LNV сказать нечего.
Оказалось, есть что. И LNV это сказал.
Вернуться в «Поговорим о математике...»
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей и 21 гость