Math.luga.ru  :  г. Луга Ленинградской области. Математический сайт
Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо
Система Orphus
Устная командная математическая олимпиада Лужского района среди 11 классов
2 октября 2006 г. в средней школе № 2 состоялась устная командная математическая олимпиада Лужского района среди 11 классов.

Задачи

1. (3 балла, 1 минута) Уравнение $2x+3y+4z=5$ задаёт в пространстве плоскость. Напишите уравнение прямой, по которой эта плоскость пересекается с координатной плоскостью $yOz$.

2. (4 балла, 3 минуты) Существует ли такой многочлен $P(x)$, отличный от константы, для которого при всех $x$ выполнено неравенство $P(x)<P^\prime(x)$ ?

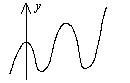
3. (3 балла, 2 минуты) Петя нарисовал график функции, задаваемой на всей числовой прямой формулой $f(x)=ax^3+bx^2+cx+d$, затем стёр ось абсцисс. После этого получилось то, что изображено на рисунке. Докажите, что Петя ошибся при построении графика.

4. (3 балла, 2 минуты) Может ли при пересечении куба плоскостью получиться в сечении восьмиугольник?

5. (4 балла, 3 минуты) Решите уравнение $\sin 3x\cdot\sin 4x=1$.

6. (4 балла, 4 минуты) Сколькими способами можно разделить 10 рублёвых монет между тремя людьми?

7. (4 балла, 3 минуты) Найдите все $k$, при которых областью определения функции, задаваемой формулой $\displaystyle f(x)=\sqrt{\cos kx-1}$, является множество всех целых чисел.

8. (4 балла, 3 минуты) Существует ли такая функция $f$, заданная на всей числовой оси, для которой $f^\prime(x+1)=f^\prime(x)+2x+1$ ?

9. (4 балла, 3 минуты) Вычислите $\sin 10^\circ \cos 20^\circ \cos 40^\circ$.

10. (4 баллов, 3 минуты) Что больше: $1{,}2345^{6789}$ или $1000$ ?

11. (4 балла, 2 минуты) Существует ли функция $f$, для которой при всех положительных $x$  выполняется равенство $f(f(x))=x^2$ ?

12. (4 балла, 2 минуты) Укажите наибольшее возможное $x$, для которого при любом натуральном $n$  выполнено неравенство $\dfrac{2n+3}{3n+4}\geqslant x$.

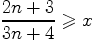13. (3 балла, 2 минуты) Может ли сумма бесконечно убывающей геометрической прогрессии быть равна её третьему члену?

14. (4 балла, 3 минуты) Приведите пример таких чисел $a$, $b$, $c$, $d$, $e$, что многочлен $P(x)=ax^4+bx^3+cx^2+dx+e$  удовлетворяет следующим условиям: $P(1)=3$, $P(2)=9$, $P(3)=19$.

15. (4 балла, 2 минуты) Изобразите множество точек пространства, координаты которых удовлетворяют уравнению $z=x^2+y^2$.

Итоговый протокол

Максимальное число баллов, которые могла набрать команда, равнялось 56.

название (номер) школы и состав команды сумма баллов место
школа № 2
Григорьев Михаил, Меженько Иван, Семёнов Сергей		27I
школа № 3
Зубанов Константин, Павлов Дмитрий, Селезнёв Максим		21II
школа № 3 (в/к-2, 10 кл.)
Александров Георгий, Ермаков Александр		19 
школа № 3 (в/к-1, 10 кл.)
Воробьёв Юрий, Ермаков Александр, Солдатов Кирилл		18 
школа № 4
Васильев Михаил, Гераскин Ратибор, Кукушкин Алексей		4III
школа № 1
Борисов Андрей, Карпенкова Анастасия, Кондрат Сергей		34

По правилам, каждая школа района заявляет для участия в УКО только одну команду, которая и определяет место школы в этом соревновании. Однако жюри обычно допускает для участия в олимпиаде и внеконкурсные команды, результаты которых не влияют на официальные показатели школы (такие команды отмечены в/к ).



  Последнее обновление 19 ноября 2006 года
Главная • Информация • ФотоАльбом • Гостевая • Форум • Письмо
© math.luga.ru, 2002–2017. Все права защищены. При цитировании ссылка обязательна