Math.luga.ru : г. Луга Ленинградской области. Математический сайт

Выездная физико-математическая олимпиада МФТИ
С. П. Павлов
 Мой бывший ученик (ныне — студент Московского физико-технического института)
В. С. Поликарпов, поступивший в МФТИ, кстати, без экзаменов как
призёр федеральной окружной олимпиады, приехав в Лугу на каникулы, привёз
с собой тексты заданий для проведения выездной олимпиады МФТИ.
Методические материалы включали в себя 9 задач по математике и 6
по физике. Оргкомитет советовал выбрать по 3 задачи каждого
предмета и провести физико-математическую олимпиаду.
Но мы решили сделать две отдельные олимпиады.
2 февраля была проведена олимпиада по физике, 3 февраля —
по математике.
Мой бывший ученик (ныне — студент Московского физико-технического института)
В. С. Поликарпов, поступивший в МФТИ, кстати, без экзаменов как
призёр федеральной окружной олимпиады, приехав в Лугу на каникулы, привёз
с собой тексты заданий для проведения выездной олимпиады МФТИ.
Методические материалы включали в себя 9 задач по математике и 6
по физике. Оргкомитет советовал выбрать по 3 задачи каждого
предмета и провести физико-математическую олимпиаду.
Но мы решили сделать две отдельные олимпиады.
2 февраля была проведена олимпиада по физике, 3 февраля —
по математике.
Условия задач по математике
1.
Десять волейбольных команд сыграли между собой турнир в один круг.
За выигрыш давалось одно очко, за проигрыш — ноль. Докажите, что
если команда, занявшая 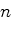 -ое место, набрала
-ое место, набрала
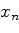 очков, то выполняется неравенство
очков, то выполняется неравенство
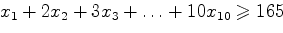 .
.
2.
Четырёхугольник 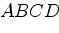 касается вписанной в него
окружности в точках
касается вписанной в него
окружности в точках 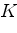 ,
,
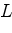 ,
,
 ,
,
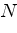 .
Точка
.
Точка  , лежащая внутри
, лежащая внутри  ,
соединена отрезками с точками
,
соединена отрезками с точками  ,
,
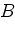 ,
,
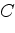 ,
,
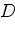 . Эти отрезки делят стороны
. Эти отрезки делят стороны
 на 8 частей, которые поочерёдно раскрашены
в два цвета — красный и синий. Докажите, что произведение
длин красных отрезков равно произведению длин синих.
на 8 частей, которые поочерёдно раскрашены
в два цвета — красный и синий. Докажите, что произведение
длин красных отрезков равно произведению длин синих.
3.
Последовательность натуральных чисел
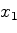 ,
,
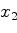 ,...,
,...,
 такова, что при
такова, что при
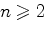 выполняется равенство
выполняется равенство
 . Найдите все
. Найдите все
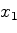 , при которых последовательность содержит число 2006.
, при которых последовательность содержит число 2006.
4.
Можно ли в клетках таблицы
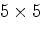 записать числа
от 1 до 25 так, чтобы разность
в любых двух соседних (по стороне) клетках была а) не больше 3;
б) не меньше 12 ?
записать числа
от 1 до 25 так, чтобы разность
в любых двух соседних (по стороне) клетках была а) не больше 3;
б) не меньше 12 ?
5.
На продолжении стороны 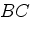 параллелограмма
параллелограмма
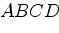 за точку
за точку 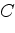 взята
точка
взята
точка 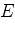 так, что
так, что
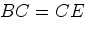 . Прямая, параллельная диагонали
. Прямая, параллельная диагонали
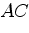 , пересекает отрезки
, пересекает отрезки 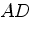 ,
,
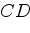 ,
, 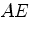 ,
,
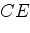 в точках
в точках
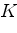 ,
, 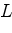 ,
,
 ,
, 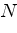 соответственно.
Докажите, что
соответственно.
Докажите, что 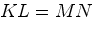 .
.
6.
Возрастающая арифметическая прогрессия состоит из натуральных чисел.
Может ли сумма 2005 последовательных членов прогрессии равняться числу
а) 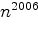 ;
б)
;
б) 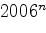 (
(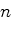 — некоторое натуральное число)?
— некоторое натуральное число)?
7.
Докажите, что если
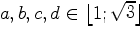 ,
то выполняется неравенство
,
то выполняется неравенство
Условия задач по физике
1.
Верёвка длины 20 м переброшена через блок. В начальный момент верёвка висит симметрично относительно вертикальной прямой, пересекающей ось блока, и покоится, затем в результате незначительного толчка начинает двигаться по блоку. Будет ли движение верёвки равномерно ускоренным? Какова будет скорость верёвки, когда она сойдёт с блока? (массой и размером блока пренебречь).
2.
В цепь, состоящую из аккумулятора и сопротивления
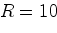 Ом включают вольтметр: сначала
последовательно, затем параллельно
Ом включают вольтметр: сначала
последовательно, затем параллельно 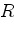 .
Оба показания вольтметра одинаковы.
Сопротивление вольтметра
.
Оба показания вольтметра одинаковы.
Сопротивление вольтметра 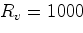 Ом.
Каково внутреннее сопротивление аккумулятора?
Ом.
Каково внутреннее сопротивление аккумулятора?
3.
В сосуд объёмом 10 л, наполненный сухим воздухом при нормальных условиях (давление 1 атм, температура 0 градусов Цельсия), вводят 3 г воды и нагревают сосуд до 100 градусов Цельсия. Определить давление влажного воздуха в сосуде при этой температуре.
4.
Человек с близорукими глазами может читать мелкий шрифт на расстоянии не более 18 см от глаз. Чему равны оптическая сила и фокусное расстояние очков, восполняющих недостаток таких близоруких глаз?
5.
Цилиндрический бак диаметром 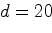 см
и высотой
см
и высотой  м наполнен водой
и посредством невесомой штанги длиной
м наполнен водой
и посредством невесомой штанги длиной 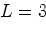 м,
неподвижно скреплённой с баком, подвешен к шарниру.
Вода вытекает из бокового отверстия площадью
м,
неподвижно скреплённой с баком, подвешен к шарниру.
Вода вытекает из бокового отверстия площадью
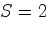 кв. см, просверленного в баке
около дна, со скоростью
кв. см, просверленного в баке
около дна, со скоростью 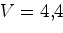 м/сек.
На какой угол от вертикали отклонится бак?
(Понижением уровня воды в баке вследствие вытекания пренебречь;
считать угол отклонения малым.)
м/сек.
На какой угол от вертикали отклонится бак?
(Понижением уровня воды в баке вследствие вытекания пренебречь;
считать угол отклонения малым.)
6.
Электромотор постоянного тока, включённый в цепь батареи с ЭДС,
равной 24 вольта, при полном сопротивлении цепи
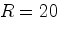 Ом делает 600 оборотов в минуту
при токе в цепи 0,2 ампера. Какую ЭДС разовьёт тот же мотор,
работая в качестве динамомашины при 1400 оборотах в минуту?
Ом делает 600 оборотов в минуту
при токе в цепи 0,2 ампера. Какую ЭДС разовьёт тот же мотор,
работая в качестве динамомашины при 1400 оборотах в минуту?
Результаты участников (математика)
Участникам олимпиады были предложены 7 задач.
По условиям, установленным оргкомитетом, любая задача оценивалась в 1 балл,
причём, выставляемые оценки могли принимать лишь одно из пяти значений:
0; 0,3; 0,6; 0,9; 1.
| Фамилия, имя участника |
класс |
школа |
сумма баллов |
место, диплом |
| Елизарова Наталья | 11 кл. | шк. № 6 | 5 | диплом I степени |
| Самсонов Глеб | 11 кл. | шк. № 3 | 4,9 | диплом I степени |
| Зубанов Константин | 10 кл. | шк. № 3 | 4,8 | диплом I степени |
| Ермаков Александр | 9 кл. | шк. № 3 | 4,2 | диплом II степени |
| Павлов Дмитрий | 10 кл. | шк. № 3 | 3,9 | диплом III степени |
| Меженько Иван | 10 кл. | шк. № 2 | 3,8 | диплом III степени |
| Расторгуев Алексей | 11 кл. | шк. № 3 | 3,3 | 4 место |
| Широков Станислав | 11 кл. | шк. № 3 | 2,5 | 5 место |
| Александров Георгий | 9 кл. | шк. № 3 | 2 | 6 место |
| Воробьёв Юрий | 9 кл. | шк. № 3 | 1,9 | 7 место |
| Селезнёв Максим | 10 кл. | шк. № 3 | 0,9 | 8 место |
| Курченков Антон | 11 кл. | шк. № 3 | 0,6 | 9–10 место |
| Харламов Алексей | 11 кл. | шк. № 3 | 0,6 | 9–10 место |
| Крючков Денис | 11 кл. | шк. № 3 | 0 | |
| Миклушов Никита | 11 кл. | шк. № 3 | 0 | |
* * *
Выражаю глубокую благодарность В. С. Поликарпову, а также
студентам мат-меха СПбГУ В. И. Щипцову и В. А. Васильеву,
принявшим активное участие в проведении олимпиады и работе жюри,
а также администрации средней школы № 3 г. Луги
за предоставленное помещение.
Последнее обновление 6 декабря 2006 года
 Мой бывший ученик (ныне — студент Московского физико-технического института)
В. С. Поликарпов, поступивший в МФТИ, кстати, без экзаменов как
призёр федеральной окружной олимпиады, приехав в Лугу на каникулы, привёз
с собой тексты заданий для проведения выездной олимпиады МФТИ.
Методические материалы включали в себя 9 задач по математике и 6
по физике. Оргкомитет советовал выбрать по 3 задачи каждого
предмета и провести физико-математическую олимпиаду.
Но мы решили сделать две отдельные олимпиады.
2 февраля была проведена олимпиада по физике, 3 февраля —
по математике.
Мой бывший ученик (ныне — студент Московского физико-технического института)
В. С. Поликарпов, поступивший в МФТИ, кстати, без экзаменов как
призёр федеральной окружной олимпиады, приехав в Лугу на каникулы, привёз
с собой тексты заданий для проведения выездной олимпиады МФТИ.
Методические материалы включали в себя 9 задач по математике и 6
по физике. Оргкомитет советовал выбрать по 3 задачи каждого
предмета и провести физико-математическую олимпиаду.
Но мы решили сделать две отдельные олимпиады.
2 февраля была проведена олимпиада по физике, 3 февраля —
по математике.